TRIANGLES Solutions of TS & AP Board Class 9 Mathematics

 9th Class Maths Solutions Chapter 7 Triangles 

Exercise:- 7.1

In quadrilateral ACBD, AC = AD and AB bisects ∠A. Show that ΔABC ≅ ΔABD What can you say about BC and BD ?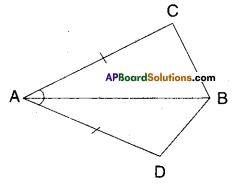

Solution:
Given that AC = AD
∠BAC = ∠BAD (∵ AB bisects∠A)
Now in ΔABC and ΔABD
AC = AD (∵ given)
∠BAC = ∠BAD (Y given)
AB = AB (common side)
∴ ΔABC ≅ ΔABD
(∵ SAS congruence rule)
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA, prove that i) ΔABD ≅ΔBAC ii) BD = AC
iii) ∠ABD = ∠BAC.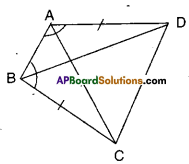

Solution :
i) Given that AD = BC and
∠DAB = ∠CBA
Now in ΔABD and ΔBAC
AB = AB (∵ Common side)
AD = BC (∵ given)
∠DAB = ∠CBA (∵ given)
∴ ΔABD ≅ ΔBAC
(∵ SAS congruence)
ii) From (i) AC = BD (∵ CPCT)
iii) ∠ABD = ∠BAC [ ∵ CPCT from (i)]
AD and BC are equal and perpendi-culars to a line segment AB. Show that CD bisects AB.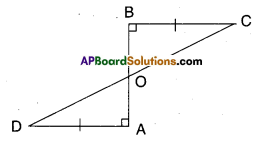

Solution:
Given that AD = BC; AD ⊥ AB; BC ⊥ AB
In ΔBOC and ΔAOD
∠BOC = ∠AOD (∵ vertically opposite angles)
∴ ΔOBC = ΔOAD (∵ right angle)
BC = AD
ΔOBC ≅ ΔOAD (∵ AAS congruence)
∴ OB = OA (∵ CPCT)
∴ ‘O’ bisects AB
Also OD = OC
∴ ‘O’ bisects CD
⇒ AB bisects CD
l and m are two parallel lines inter-sected by another pair of parallel lines p and q. Show that ΔABC ≅ ΔCDA.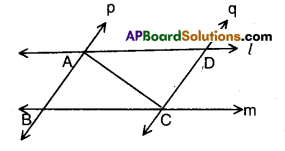

Solution:
Given that l // m; p // q.
In ΔABC and ΔCDA
∠BAC = ∠DCA (∵ alternate interior angles)
∠ACB = ∠CAD
AC = AC
∴ ΔABC ≅ ΔCDA (∵ ASA congruence)
In the figure given below AC = AE; AB = AD and ∠BAD = ∠EAC. Show that BC = DE.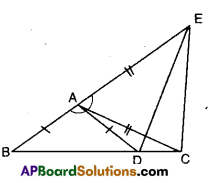

Solution:
Given that AC = AE, AB = AD and
∠BAD = ∠EAC
In ΔABC and ΔADE
AB = AD
AC = AE
∠BAD = ∠EAC
∴ ΔABC ≅ ΔADE (∵ SAS congruence)
⇒ BC = DE (CPCT)
In right triangle ABC, right angle is at ‘C’ M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see fig.). Show that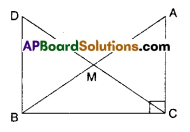

i) ΔAMC = ΔBMD
ii) ∠DBC is a right angle
iii) ΔDBC = ΔACB
iv) CM = 12 AB
Solution:
Given that ∠C = 90°
M is mid point of AB;
DM = CM (i.e., M is mid point of DC)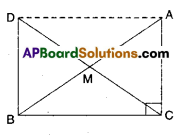

i) In ΔAMC and ΔBMD
AM = BM (∵ M is mid point of AB)
CM = DM ( ∵ M is mid point of CD)
∠AMC = ∠BMD ( ∵ Vertically opposite angles)
∴ ΔAMC ≅ ΔBMD
(∵ SAS congruence)
(CPCT of ΔAMC and ΔBMD)
But these are alternate interior angles for the lines DB and AC and DC as transversal.
∴DB || AC
As AC ⊥ BC; DB is also perpendicular to BC.
∴ ∠DBC is a right angle.
DB = AC (CPCT of ΔBMD and ΔAMC)
∠DBC = ∠ACB = 90°(already proved)
BC = BC (Common side)
∴ ΔDBC ≅ ΔACB (SAS congruence rule)
 DC = 12 AB (Dividing both sides by 2)
CM = 12AB
In the given figure ΔBCD is a square and ΔAPB is an equilateral triangle.
Prove that ΔAPD ≅ ΔBPC.
[Hint: In ΔAPD and ΔBPC; 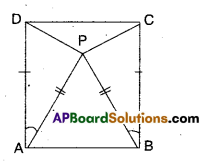AD¯¯¯¯¯¯¯¯¯=BC¯¯¯¯¯¯¯¯, AP¯¯¯¯¯¯¯¯=BP¯¯¯¯¯¯¯¯ and ∠PAD = ∠PBC = 90° – 60° = 30°]

Solution:
Given that □ABCD is a square.
ΔAPB is an equilateral triangle.
Now in ΔAPD and ΔBPC
AP = BP ( ∵ sides of an equilateral triangle)
AD = BC (∵ sides of a square)
∠PAD = ∠PBC [ ∵ 90° – 60°]
∴ ΔAPD ≅ ΔBPC (by SAS congruence)
In the figure given below ΔABC is isosceles as AB¯¯¯¯¯¯¯¯=AC¯¯¯¯¯¯¯¯¯;BA¯¯¯¯¯¯¯¯ and CA¯¯¯¯¯¯¯¯¯ are produced to Q and P such that AQ¯¯¯¯¯¯¯¯¯=AP¯¯¯¯¯¯¯¯. Show that PB¯¯¯¯¯¯¯¯=QC¯¯¯¯¯¯¯¯¯ .
(Hint: Compare ΔAPB and ΔACQ)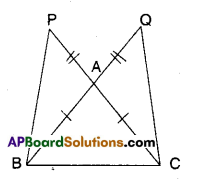

Solution:
Given that ΔABC is isosceles and
AP = AQ
Now in ΔAPB and ΔAQC
AP = AQ (given)
AB = AC (given)
∠PAB = ∠QAC (∵ Vertically opposite angles)
∴ ΔAPB ≅ ΔAQC (SAS congruence)
∴ PB¯¯¯¯¯¯¯¯=QC¯¯¯¯¯¯¯¯¯ (CPCT of ΔAPB and ΔAQC)
In the figure given below AABC, D is the midpoint of BC. DE ⊥ AB, DF ⊥ AC and DE = DF. Show that ΔBED ≅ AΔCFD.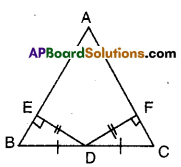

Solution:
Given that D is the mid point of BC of ΔABC.
DF ⊥ AC; DE = DF
DE ⊥ AB
In ΔBED and ΔCFD
∠BED = ∠CFD (given as 90°)
BD = CD (∵D is mid point of BC)
ED = FD (given)
∴ ΔBED ≅ ΔCFD (RHS congruence)
If the bisector of an angle of a triangle also bisects the opposite side, prove that the triangle is isosceles.
Solution: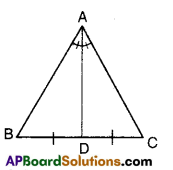

Let ΔABC be a triangle.
The bisector of ∠A bisects BC
To prove: ΔABC is isosceles
(i.e., AB = AC)
We know that bisector of vertical angle divides the base of the triangle in the ratio of other two sides.
∴ 
Thus ABAC = 1( ∵ given)
⇒ AB = AC
Hence the Triangle is isosceless.
In the given figure ΔABC is a right triangle and right angled at B such that ∠BCA = 2 ∠BAC. Show that the hypotenuse AC = 2BC.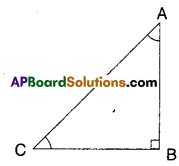

[Hint : Produce CB to a point D that BC = BD]
Solution: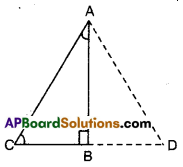

Given that ∠B = 90°; ∠BCA = 2∠BAC
To prove : AC = 2BC
Produce CB to a point D such that
BC = BD
Now in ΔABC and ΔABD
AB = AB (common)
BC = BD (construction)
∠ABC =∠ABD (∵ each 90°)
∴ ΔABC ≅ ΔABD
Thus AC = AD and ∠BAC = ∠BAD = 30° [CPCT]
[ ∵ If ∠BAC = x then
∠BCA = 2x
x + 2x = 90°
3x = 90°
⇒ x = 30°
∴ ∠ACB = 60°]
Now in ΔACD,
∠ACD = ∠ADC = ∠CAD = 60°
∴∠ACD is equilateral ⇒ AC = CD = AD
⇒ AC = 2BC (∵ C is mid point)
 Exercise 7.2
Question 1.
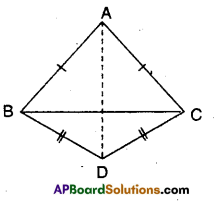
In an isosceles triangle ABC, with AB = AC, the bisectors of ∠B and ∠C intersect each other at ‘O’. Join A to O. Show that (i) OB = OC (ii) AO bisects ∠A.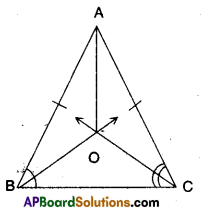

Solution:
Given that in ΔABC
AB = AC
Bisectors of ∠B and ∠C meet at ‘O’.
To prove
i) OB = OC
∠B = ∠C (Angles opposite to equal, sides)
12∠B=12∠C (Dividing both sides by 2)
∠OBC = ∠OCB
⇒ OB = OC (∵ Sides opposite to equal angles in ΔOBC)
ii) AO bisects ∠A.
In ΔAOB and ΔAOC
AB = AC (given)
BO = CO (already proved)
∠ABO = ∠ACO (∵ ∠B =∠C)
∴ ΔAOB ≅ ΔAOC
⇒ ∠BAO = ∠CAO [ ∵ CPCT of ΔAOB and ΔAOC]
∴ AO is bisector of ∠A.

Question 1.

Question 2.

Question 3.

Question 4.

Question 5.

Question 6.

ii) ∠MDB = ∠MCA

iii) In ΔDBC and ΔACB

iv) DC = AB (CPCT of ΔDBC and ΔACB)

Question 7.

Question 8.

Question 9.

Question 10.

Question 11.

Question 2.
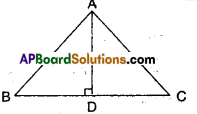
In ΔABC, AD is the perpendicular bisector of BC (see given figure). Show that ΔABC is an isosceles triangle in which AB = AC

Solution:
Given that AD ⊥ BC; AD = DC
In ΔABD and ΔACD
AD = AD (common)
BD = DC (given)
∠ADB = ∠ADC (given)
∴ ΔABD ≅ ΔACD (∵ SAS congruence)
⇒ AB = AC (CPCT of ΔABD and ΔACD)

Question 3.
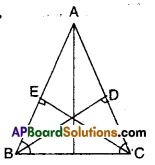
ABC is an isosceles triangle in which altitudes BD and CE are drawn to equal sides AC and AB respectively (see figure). Show that these altitudes are equal.

Solution:
Given that AC = AB; BD ⊥ AC; CE ⊥ AB
In ΔBCD and ΔCBE
∠BDC = ∠CEB (90° each)
∠BCD = ∠CBE (∵ angles opp. to equal sides of a triangle)
BC = BC
∴ ΔBCD ≅ ΔCBE (∵ AAScongruence)
⇒ BD = CE (CPCT)



Question 4.
ABC is a triangle in which altitudes BD and CE to sides AC and AB are equal (see figure). Show that
i) ΔABD ≅ ΔACE
ii) AB = AC i.e., ABC is an isosceles triangle.

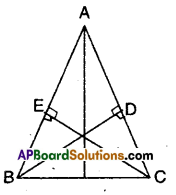
Solution:
Given that BD ⊥ AC; CE ⊥ AC
BD = CE
Now in ΔABD and ΔACE
∠ADB = ∠AEC (∵ given 90°)
∠A = ∠A (commori angle)
BD = CE
∴ ΔABD = ΔACE (∵ AAS congruence)
⇒ AB = AC (∵ C.P.C.T)

Question 5.
ΔABC and ΔDBC are two isosceles triangles on the same base BC (see figure). Show that ∠ABD = ∠ACD.

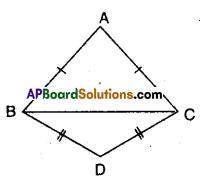
Solution:

Given that ΔABC and ΔDBC are isosceles.
To prove ∠ABD = ∠ACD
Join A and D.
Now in ΔABD and ACD
AB = AC (∵ equal sides of isosceles triangles)
BD = CD (∵ equal sides of isosceles triangles)
AD = AD (∵ common side)
∴ ΔABD ≅ ΔACD (∵ SSS congruence)
⇒ ∠ABD = ∠ACD (CPCT)

Exercise 7.3

Question 1.
AD is an altitude of an isosceles triangle ABC in which AB = AC. Show that, (i) AD bisects BC (ii) AD bisects ∠A.
Solution: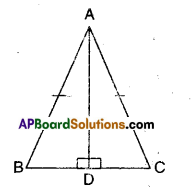

Given that in ΔABC, AB = AC
and AD ⊥ BC
i) Now in ΔABD and ΔACD
AB = AC (given)
∠ADB = ADC (given AD ⊥ BC)
AD = AD (common)
∴ ΔABD ≅ ΔACD (∵ RHS congruence)
⇒ BD = CD (CPCT)
⇒ AD, bisects BC.

ii) Also ∠BAD = ∠CAD
(CPCT of ΔABD ≅ ΔACD )
∴ AD bisects ∠A.

Question 2.
Two sides AB, BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see figure). Show that:
(i) ΔABM ≅ ΔPQN
ii) ΔABC ≅ ΔPQR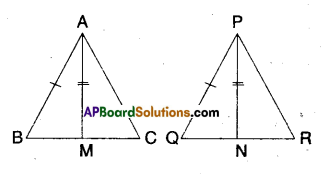

Solution:
Given that
AB = PQ
AM = PN
i) Now in ΔABM and ΔPQN
AB = PQ (given)
AM = PN (given)
BM = QN (∵ BC = QR ⇒ 12BC = 12QR ⇒ BM = QN)
∴ ΔABM ≅ ΔPQN
(∵ SSS congruence)

ii) In ΔABC and ΔPQR
AB = PQ (given)
BC = QR (given)
∠ABC = ∠PQN [∵ CPCT of ΔABM and ΔPQN from (i)]
∴ ΔABC ≅ ΔPQR
(∵ SAS congruence)

Question 3.
BE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
Solution: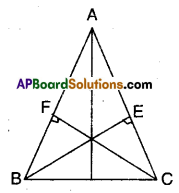

In ΔABC altitude BE and CF are equal.
Now in ΔBCE and ΔCBF
∠BEC = ∠CFB (∵ given 90°)
BC = BC (common; hypotenuse)
CF = BE (given)
∴ ΔBEC ≅ ΔCBF
⇒ ∠EBC = ∠FCB (∵ CPCT)
But these are also the interior angles opposite to sides AC and AB of ΔABC.
⇒ AC = AB
Hence proved.

Question 4.
ΔABC is an isosceles triangle in which AB = AC. Show that ∠B = ∠C.
(Hint : Draw AP ⊥ BQ (Using RHS congruence rule)
Solution: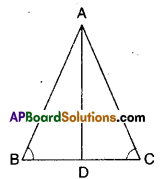

Given the ΔABC is an isosceles triangle and AB = AC
Let D be the mid point of BC; Join A, D.
Now in ΔABD and ΔACD
AB = AC (given)
BD = DC (construction)
AD = AD (common)
∴ ΔABD ≅ ΔACD (∵ SSS congruence)
⇒ ∠B = ∠C [∵ CPCT]

Question 5.
ΔABC is an isosceles triangle in which AB = AC. Side BA is produced to D such that AD = AB (see figure). Show that ∠BCD is a right angle.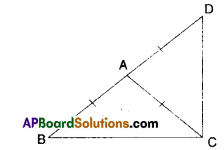

Solution: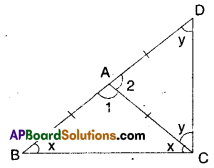

Given that in ΔDBC; AB = AC; AD = AB
In ΔABC
∠ABC + ∠ACB = ∠DAC …………… (1)
[∵ exterior angle]
In ΔACD
∠ADC + ∠ACD = ∠BAC ………………(2)
Adding (1) & (2)
∠DAC + ∠BAC = 2 ∠ACB + 2∠ACD
[∵ ∠ABC = ∠ACB
∠ADC = ∠ACD]
180° = 2 [∠ACB + ∠ACD]
180° = 2[∠BCD]
∴ ∠BCD = 180∘2 = 90°
(or)
From the figure
∠2 = x + x = 2x
∠1 = y + y = 2y
∠1 + ∠2 = 2x + 2y
180° = 2 = (x + y)
∴ x + y  = 180∘2 = 90°
Hence proved.

Question 6.
ABC is a right angled triangle in which ∠A = 90° and AB = AC, Show that ∠B = ∠C.
Solution: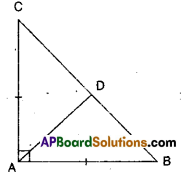

Given ΔABC; AB – AC
Join the mid point D of BC to A.
Now in ΔADC and ΔADB
AD = AD (common)
AC = AB (giyen)
DC = DB (construction)
⇒ ΔADC ≅ ΔADB
⇒ ∠C = ∠B (CPCT)

Question 7.
Show that the angles of an equilateral triangle are 60° each.
Solution: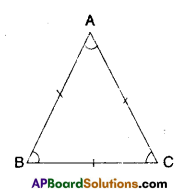

Given ΔABC is an equilateral triangle
AB = BC = CA
∠A = ∠B (∵ angles opposite to equal sides)
∠B = ∠C (∵ angles opposite to equal sides)
⇒ ∠A = ∠B = ∠C = x say
Also ∠A+∠B + ∠C =180°
⇒ x + x + x = 180°
3x = 180°
⇒ x = 1803 = 60°
Hence proved.

Triangles Exercise 7.4

Question 1.
Show that in a right angled triangle, the hypotenuse is the longest side.
Solution: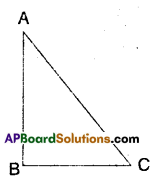

Let a ΔABC be right angled at ∠B.
Then ∠A + ∠C = 90°
(i.e.,) ∠A and ∠C are both acute.
Now, ∠A < ∠B ⇒ BC < AC
Also ∠C < ∠B ⇒ AB < AC
∴ AC, the hypotenuse is the longest side.

Question 2.
In the given figure, sides AB and AC of ΔABC are extended “to points P and Q respectively. Also ∠PBC < ∠QCB. Show that AC > AB.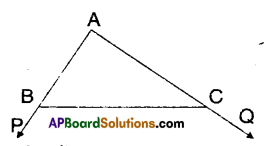

Solution:
From the figure,
∠PBC = ∠A + ∠ACB
∠QCB = ∠A + ∠ABC
Given that ∠PBC < ∠QCB
⇒∠A + ∠ACB < ∠A + ∠ABC
⇒ ∠ACB < ∠ABC
⇒ AB < AC
⇒ AC > AB
Hence proved.

Question 3.
In the given figure, ∠B < ∠A and ∠C < ∠D. Show that AD < BC.

Solution:
Given that ∠B < ∠A; ∠C < ∠D
∠B < ∠A ⇒ AO < OB [in ΔAOB] ……………… (1)
∠C < ∠D ⇒ OD < OC [in ΔCOD]…… (2)
Adding (1) & (2)
AO + OD < OB + OC
AD < BC
Hence proved.

 

Question 4.
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see figure). Show that ∠A >∠C and ∠B > ∠D.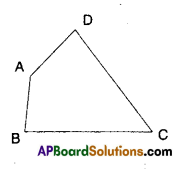

Solution: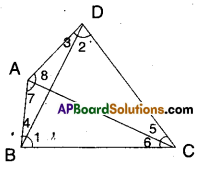

Given that AB and CD are the smallest and longest sides of quadrilateral ABCD.
From the figure,
In ΔBCD
∠1 > ∠2 [∵ DC > BC] ………………(1)
In ΔBDA
∠4 > ∠3 [∵ AD > AB] ………….(2)
Adding (1) & (2)
∠1 + ∠4 > ∠2 + ∠3
∠B > ∠D
Similarly,
In ΔABC, ∠6 < ∠7 [ ∵AB < BC] ……………….(3)
In ΔACD
∠5 < ∠8 …………. (4)
Adding (3) & (4)
∠6 + ∠5 < ∠7 + ∠8
∠C < ∠A ⇒ ∠A > ∠C
Hence proved.

Question 5.
In the given figure, PR > PQ and PS bisects ∠QPR. Prove that
∠PSR > ∠PSQ.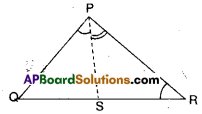

Solution:
Given that PR > PQ;
∠QPS =∠RPS
PR> PQ
∠Q > ∠R
Now ∠Q +∠QPS > ∠R + ∠RPS
⇒ 180° – (∠Q + ∠QPS) < 180° – (∠R + ∠RPS)
⇒ ∠PSQ < ∠PSR ⇒ ∠PSR > ∠PSQ
Hence proved.

Question 6.
If two sides of a triangle measure 4 cm and 6 cm find all possible measurements (positive integers) of the third side. How many distinct triangles can be obtained ?
Solution:
Given that two sides of a triangle are 4 cm and 6 cm.
∴ The measure of third side > Differ-ence between other two sides.
third side > 6 – 4
third side > 2
Also the measure of third side < sum of other two sides
third side <6 + 4 < 10
∴ 2 < third side <10
∴ The measure of third side may be 3 cm, 4 cm, 5 cm, 6 cm, 7 cm, 8 cm, 9 cm
∴ Seven distinct triangles can be obtained.

Question 7.
Try to construct a triangle with 5 cm, 8 cm and 1 cm. Is it possible or not ? Why ? Give your justification.
Solution:
As the sum (6 cm) of two sides 5 cm and 1 cm is less than third side. It is not possible to construct a triangle with the given measures.